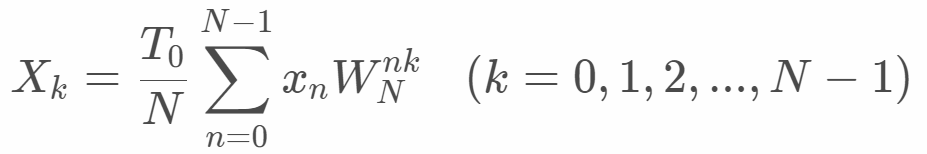
はじめに
1年前ごろにフーリエ変換について一度概観しました。高速フーリエ変換(FFT)を実装できる程度に理解したいと思っています。しかし、高速フーリエ変換の前段の離散フーリエ変換が全くわからず、2023年の年明けごろから再チャレンジ(3回目くらい)しており、ようやく理解しつつあるので、私の理解を連載形式で記述していきます。気になる点などあれば、本記事やTwitterでコメントお願いします。
参考情報
いろいろな書籍や記事などに目を通して、わからん続きでしたが、個人的には以下3つの資料で理解が深まりました。上から順番に読むことをオススメします。
| No | 名前 | コメント |
|---|---|---|
| 1 | 数学ガールの秘密ノート/丸い三角関数 | 三角関数とは何かについて理解を深められます。三角の背景に円がイメージできるようになります。 |
| 2 | 数学ガールの物理ノート/波の重ね合わせ | 波を数式で記述することについて理解を深められます。本書で離散フーリエ変換の理解が進むと確信しました。 |
| 3 | おそらく富山大学の離散フーリエ変換教材 | 大変丁寧に一歩ずつ説明してくれています。行列表現と例示でかなり理解が深まりました。 |
離散フーリエ変換とは
ChatGPTによる概要

この説明は妥当と思います。最後の離散フーリエ変換の使われ方については、実際には高速フーリエ変換での利用となる、くらいの補足が必要かなと思いました。
超ざっくりな概要だと、波形データ(離散的な時間領域の信号)を入力すると、その波形に含まれる周波数の特徴(離散周波数スペクトル密度)を得られる変換手法です。周波数の特徴が解るとその特徴を踏まえていろいろ処理することができ、良い感じの結果、応用ができるという感じです。その応用として音声処理や画像処理分野などになります。
離散フーリエ変換の解釈、読み方
本編です。上記の数式分解していきます。
O(N^2)を見つける
プログラミング実装の観点で離散フーリエ変換は遅いです。それは計算量がO(N^2)のためです。雑な説明だとfor文の二重ループが存在するアルゴリズムだからです。それでは、離散フーリエ変換の数式から二重ループを見つけます。
1つ目は、Σの部分です。これは見つけやすいです。
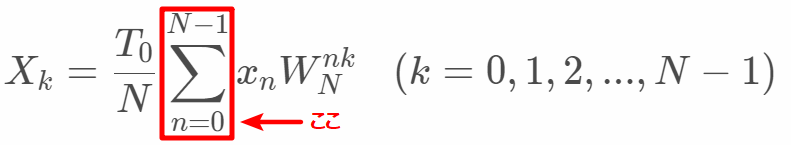
2つ目は(k=0,1,2,...,N-1)の部分です。最初イメージしにくかったのですが、XはN個(サンプリングデータ)のデータ列となります*1。そのN個それぞれにΣの計算をします。つまりこれで、O(N^2)です!
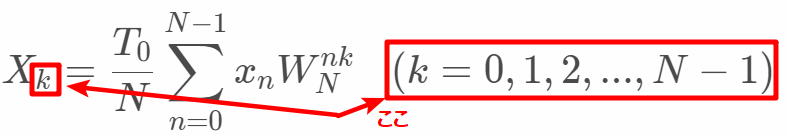
計算結果を考える
XがN個であることは離散フーリエ変換の計算結果でもあります。離散フーリエ変換の結果は入力に対して、出力/結果は例えば"2"と一個で求められるわけではありません。サンプリングデータ数(N個)のデータ列(一次元配列)が、出力になります。
W(DFT行列)を読む
離散フーリエ変換の数式の右端にあるWはDFT行列と名付けられています。これは以下でN*Nの行列になります。
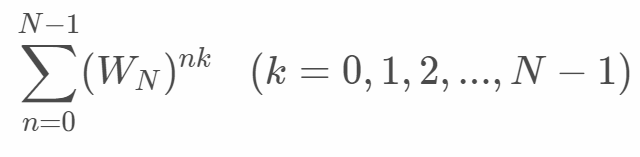
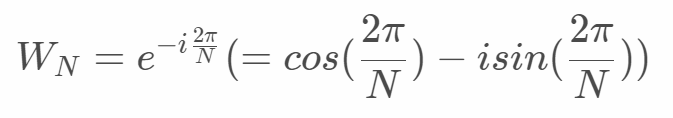
このDFT行列を理解することが離散フーリエ変換を理解することと言っても過言ではないと思います。また、このDFT行列を工夫することで高速フーリエ変換に繋がると思われます。それではDFT行列を読みます。
例示は理解の試金石として、N=4でDFT行列を示すと以下になります。DFT行列はサンプリングデータ数に応じて一意に決まります。入力データには依存しません。

1行目はk=0のため、乗数はすべて0*nとなり、0です。2行目はk=1のため、乗数は1*nです。3行目はk=2のため、乗数は2*nです。4行目はk=3のため、乗数は3*nです。
ここで、以下の関係式を用います。オイラーの公式でcosとsinに変換したとき、N乗の場合分母のNと約分されてcosの1だけが残ります。単位円で考えると回転する様子を視覚的にイメージできます。詳しくは先のPDFを参照ください。
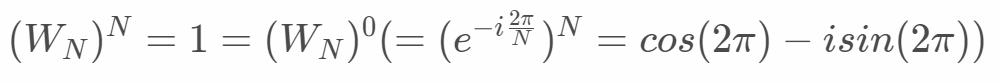
変換したDFT行列は以下になります。
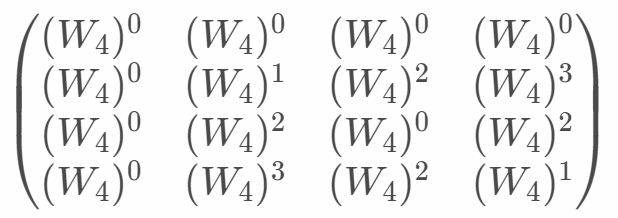
DFT行列を整理できたので、各Wの値を求め、代入します。それぞれのWは以下になります。sinとcosに分解した式から考えることで求められます。
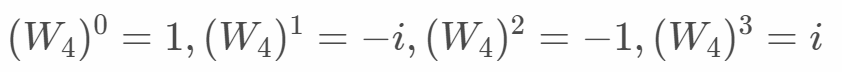

N=4のDFT行列が求まりました。離散フーリエ変換では以下のようにDFT行列をサンプリングデータxに掛け算する演算となります。そこで求められたデータ列Xが離散フーリエ変換の結果で離散周波数スペクトル密度です。

おわりに
離散フーリエ変換の数式をようやく理解できた気がします。具体的には、O(N^2)になる理由、sinとcosの要素に分解されること、実装方針などを把握できたと思います。次は実装を行いたいと思います。合わせて今回記述できていない、数値の単位及び計算結果の意味解釈も考えます。以上です、ここまでお付き合いいただきありがとうございました。
*1:kの下付き文字は省略しています。数式埋め込みを横着しているためです。
